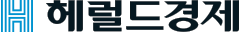이는 조선시대 10대 초반 도령들이 푸는 수학문제이다. ‘지금 사람들이 은(銀)을 나눠 가지는데, 1명당 7냥(兩)씩 나누어 가지면 4냥이 남고, 1명당 9냥씩 나누어 가지면 12냥이 부족하다. 사람 수와 은의 총수량은 각각 얼마일까?’라는 물음이다.

10일 성균관대 대동문화연구원 강민정 수석연구원에 따르면, 이 문제는 19세기 조선의 대표적인 천문ㆍ산학가 중 한 사람인 남병길(1820~1869)의 수학서 ‘산학정의(算學正義)’ 중 ‘영뉵술(盈朒術)’의 첫째 예제이다.
우리 중학생들은 잽싸게, 사람 수를 x라 하고, 은의 총수량을 y라 하면, y=7x+4…①, y=9x-12…②라고 방정식을 제시한 뒤, ②식에서 ①식을 빼면, 0=2x-16, 따라서 x=8…③, ③을 ①에 대입하면, y=(7×8)+4=60. 그래서 사람수는 8명, 은의 총수량은 60개라는 답을 내놓을 것이다.
우리 아이들은 이 방정식 만이 정확하고도 보편적으로 적용할 수 있는 유일한 해법이라 생각하거나, 이것만이 가장 바람직한 계산 방법이라고 생각할 가능성이 높다.
그러나 우리 조상들은 지름길을 알고 있었다. 두 사례의 1인당 받는 차이와 총인원이 받은 차이 만으로 쉽게 답을 구했다. ‘산학정의’ 정답편은 간략하게 원리를 설명한 뒤, 두 개 조건, 두 개 변인의 비례 관계만 이용해 다음과 같은 해법을 내놓았다.
‘1명당 받는 차이 ‘9냥-7냥=2냥(1명)’, 총인원이 받는 차이 ‘4냥+12냥=16냥’, 나눠가질 인원은 1명×16냥÷2냥=8명, 은의 총수량은 8명×7냥+4냥=60냥.’
강 수석연구원은 이처럼 ‘남을 때의 조건(盈)’과 ‘부족할 때의 조건(朒)’을 가지고 딱 맞는 수를 구하되, 문자를 사용하지 않고 숫자의 사칙연산만으로 해답을 구하는 계산법을 영뉵술(盈朒術) 또는 영부족술(盈不足術)이라고 칭했다고 전한다.
영뉵술은 동아시아 전통 수학의 비조로 일컬어지는 ‘구장산술(九章算術)’에 자세히 기록돼 있고, 이는 9세기에 아랍에 전해지고 12세기에 유럽으로 전해져, 이중가정법(method of double false position)의 기원이 되었다고 한다.
‘수포(수학포기) 극복 방안’에 대한 논의가 한창인 가운데, 최근 학교 수학에서도 ‘문제 해결 능력’ 고양을 중요한 목표로 삼아 학생들이 단일한 해법을 수동적으로 습득하기보다 다양한 풀이법을 능동적으로 모색하도록 하는데 교육 중점이 옮겨지고 있다.
‘달콤한 수학사’라는 책을 추천한 박창균 교수는 “수학 강국이라고 일컬어지는 나라들이 가지고 있는 것은 ‘수학 문화’이기 때문이다. 곧, 수학적으로 사고하는 것이 일상화되어 있고, 자국이 배출한 수학자들의 업적을 다양하게 조명하고 기리는 등 그들 문화 속에 녹아들어 있는 것”이라고 강조했다.
차분히 우리의 전통 명절을 마무리 시점, 수학을 다른 과목에 비해 좋아하지 않는 자녀와 함께 상경하는 길에, ‘생활 속의 수학문화’라는 키워드도 한 번 쯤 찬찬히 되새겨보자.
abc@heraldcorp.com
▶조선시대 수학자이자 천문학자인 남병길의 ‘산학정의’ 본문.[출처=한국민족문화대백과]